Stammtischmathe
Aushang und Aussagen

In Charlottenburg ist mir dieser Aushang an einer Kneipe aufgefallen und hat mich dazu motiviert, sich einmal mit schlecht zu Papier gebrachter Stammtischmathematik auseinanderzusetzen. Direkt frage ich mich, warum “eine” groß und fett gedruckt wurde statt “Jahren”. Aber lasst uns die Aussagen des Aushangs einmal zusammenfassen:
- Eure Lernkurve ist eine waagerechte Asymptote gegen null.
- Eine Funktion zur Bezeichnung des Politikerverstandes.
- Hausverbot für die Zugehörigkeit zu einigen Parteien und Gesundheitsbehörden.
Zu Aussage 1): eine waagerechte Asymptote bezeichnet generell eine Gerade, der sich der Wert einer Funktion im Unendlichen nähert. Dabei ist nicht ganz klar, auf wessen Lernkurve sich das asymptotische Verhalten bezieht - auf Politiker, den Leser und Wähler der Parteien,…? Aussage 2) lässt vermuten, dass die Politiker gemeint sind, da die beschriebene Hyperbelfunktion im Zusammenhang mit einer waagerechten Asymptote (0) steht und den Politikerverstand beschreibt. Als x-Achse wird nach dieser Aussage die Zeit gesetzt, als y-Achse das “Lernen”.
Asymptoten und asymptotische Funktionen
Hier fangen die mathematischen Wirrungen jedoch an. Wie oben beschrieben, bezeichnet die Asymptote nicht eine Funktion, sondern eine Gerade, der sich eine Funktion im Unendlichen annähert. Für die vertikale Annäherung wäre also die Asymptote einfach x = 0, also eine stetig nicht existierende Lernkurve (nach Aussage 1)) und damit eher “Lernlinie”. Vermutlich meint der Autor mit der Aussage eigentlich die asymptotische Funktion. Dies würde jedoch auch bedeuten, dass zu einem Zeitpunkt x = 0 das Lernen maximal, also bei 1 war. Diese Lernkurve hat dann ab einem Zeitpunkt rapide abgenommen, und geht jetzt gegen null.
Für eine konkrete Grafik zu Aussage 1 hilft hier der Zusatz “seit Jahren”, weshalb der Startzeitpunkt als zwischen fünf und zehn Jahren angenommen wird. Wenn wir die Funktion einmal plotten, resultiert das in folgender Grafik:
Als Definition von Aussage 1) folgt im Aushang nun die Funktion aus Aussage 2). Diese zeigt auch das besagte asymptotische Verhalten, jedoch bezogen auf den Politikerverstand und die Anzahl an Politikern. Die Aussage 1), die auf der x-Achse “Zeit” und y-Achse “Lernen” gesetzt hat, ist damit eigentlich hinfällig. In der nächsten Grafik sehen wir einmal die nach Aussage 2) geplottete Funktion. Die Wertemenge sind die natürlichen Zahlen (1,2,3,…), was zum Glück der Politiker bedeutet, dass es keine Halben von ihnen gibt.
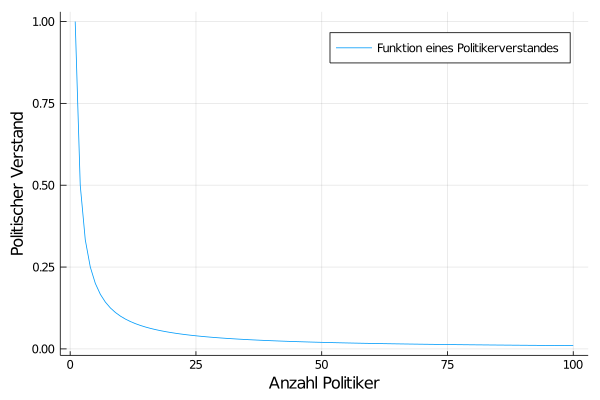
Schlussfolgerungen
Als Aussage dieser Funktion ist interessant, dass ein einzelner Politiker den höchstmöglichen politischen Verstand besitzt, und dieser mit zunehmender Anzahl stark absinkt. Der Wirkmechanismus dieser Aussage ist zweifelhaft, würde aber interessante Folgen mit sich bringen. So würde, wenn die Funktion den Verstand der einzelnen Politikers beschreibt, der Verstand der Politiker insgesamt immer eins bleiben - ob nun f(1 Politiker) = 1 Verstand oder für vier Politiker f(4 Politiker) = 0.25 Verstand, die Summe des politischen Verstands bleibt 1. Falls der politische Verstand jedoch die Summe über alle Politiker bezeichnet, sähe es schwarz für uns aus. Als Beispiel mit dem aktuellen Bundestag hätten wir dann nur f(709) = 0.0014 politischen Verstand, eine erschreckend geringe Zahl.
Zusammengefasst hat der Autor die Grenzen der Funktion in Aussage 2) ordentlich gesetzt und eine sinnvolle Wertemenge angegeben. Fragwürdig ist die Verwirrung zwischen zwei Konzepten, die an sich im Zusammenhang mit einer Asymptote stehen:
- Die “Lernkurve”, also die Zunahme an Wissen. Vermutlich wurde hier fälschlicherweise die Asymptote selbst bezeichnet und nicht die Funktion.
- Der Politische Verstand als Hyperbel beschrieben, wobei hier eine Ausdifferenzierung des Wirkmechanismus wünschenswert wäre.
Stilkritik
Insgesamt fehlt eine genauere Definition, was die Funktion eigentlich beschreibt - die Lernkurve oder politischer Verstand? Und was sollen Politiker lernen? Generell riecht der Aushang natürlich etwas nach Querdenkerei, auch die Ausschlussliste aus Aussage 3) an politischen Parteien stellen mehr oder weniger den politischen Mainstream dar. Durch den Einbezug von WHO und RKI bekommt das ganze eine Note von COVID-19, aber “seit Jahren” impliziert, dass es schon vorher ein Problem gab. Vielleicht war also Corona doch ein Inside Job, um uns klein zu halten?! Mein Fazit: klassische Stammtischmathematik mit der Absicht, durch den Einsatz von hochgestochenem Vokabular Hau-Drauf-Aussagen plausibler erscheinen zu lassen.